
Förstärkare
Illustration av förstärkare och input-voltage
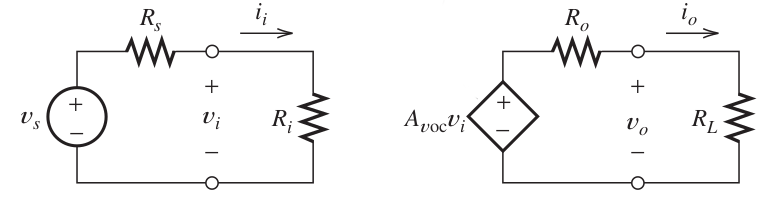
Input voltage
`V_i = R_i/(R_i+R_s)*V_s`Output voltage
`V_o = R_L/(R_o + R_L)*A_(v o c)V_i`Förstärkning relativt source
`A_(vs) = V_o/V_s`Förstärkning relativt input-voltage
`A_v = V_o/V_i`Current gain
`A_i = I_o/I_i = (v_o/R_L)/(v_i/R_i) = A_v R_i/R_L`Power gain
`G = P_o/P_i = (V_oI_o)/(V_iI_i) = A_vA_i = (A_v)^2 R_i/R_L`| Amplifier type | `R_i` | `R_o` | Gain |
|---|---|---|---|
| Voltage | `oo` | `0` | `A_(v o c)` |
| Current | `0` | `oo` | `A_(i s c)` |
| Transconductance | `oo` | `oo` | `G_(m s c)` |
| Transresistance | `0` | `0` | `R_(m o c)` |
`R < 100 Ω` brukar räknas som `0`, `R > 1MΩ` som `oo`.
Observera att det är relationen mellan `R_i` och `R_o` som bestämmer
Förstärkare i serie (cascade connection)
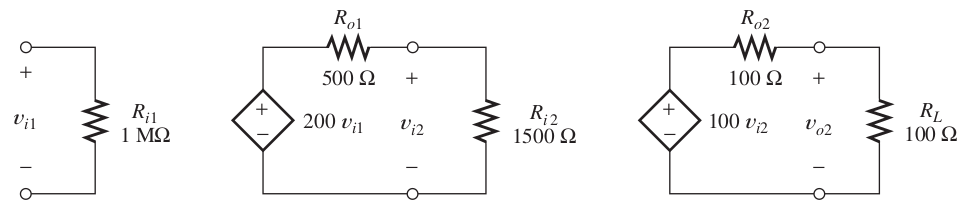
`A_v = A_(v_1)*A_(v_2)`
Obs! Glosa för kondensator/induktor
Parallell impedans[Ω]
`Z_t = 1/(1/Z_1+1/Z_2)`Seriell impedans[Ω]
`Z_t=Z_1+Z_2`Differential amplifier
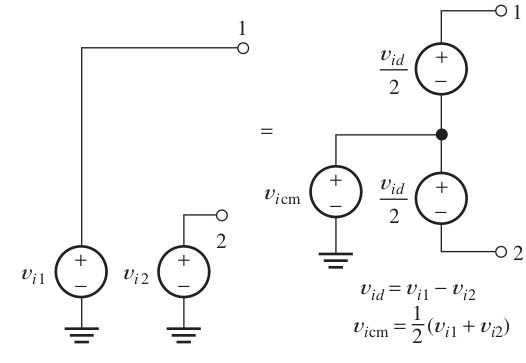
Differential signal
`v_(id) = v_(i_1) - v_(i_2)`Differential gain
`v_o = A_d v_(id)`Common mode signal
`v_(i c m) = 1/2(v_(i_1) + v_(i_2))`Common-Mode Rejection Ratio
`v_o = A_d v_(id) + A_(cm) v_(i c m)`Common-mode rejection ratio
`CMR R = 20*log_10(|A_d|/|A_(cm)|)`Operational Amp
Voltage follower
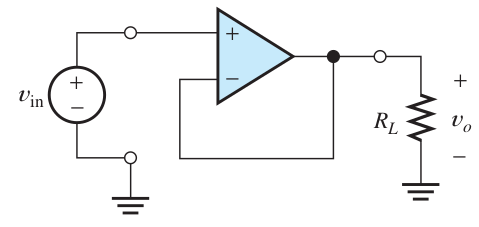
Transistorer
MOSFET regioner
| Region | Villkor |
|---|---|
| Triode region | `V_(DS) < V_(GS) - V_(t o) ^^ V_(GS) >= V_(t o)` |
| Saturation region | `V_(GS) >= V_(t o) ^^ V_(DS) >= V_(GS) - V_(t o)` |
| Cutoff region | `i_D = 0 iff V_(GS) < V_(t o)` |
Analog/Digital omvandling (ADC)
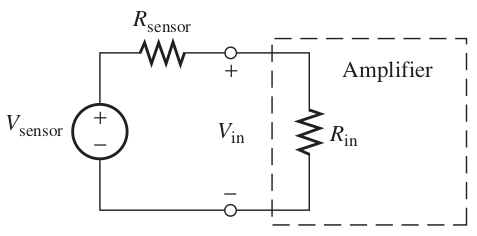
Voltage från en sensor
`V_in = V_(bb"sensor") R_(i n)/(R_(i n)+R_(bb"sensor"))`Samlingsteoremet
För att bevara all information bör samlingsfrekvensen vara `f_s > 2*f_(max)`Antal bitar för noggrann mätning
`n = Log(p)/Log(2)`